切换主题
第一章、函数与映射
第一节、映射与函数
一、映射
1、映射
2、映射的分类
X中元素不可以剩余,Y中元素可以剩余
二、函数
1、概念
2、函数特性
3、反函数、复合函数、初等函数
第二节、数列的极限
一、数列极限的定义
二、收敛数列的性质
1、唯一性
$\hspace{8em}\forall \epsilon>0,\exists N_2 \in N_+,当n>N时,总有|x_n-b|<\epsilon $
2、有界性
3、保号性
4、收敛数列与其子数列间的关系
第三节、函数的极限
一、函数极限定义
1、自变量x趋于无穷大时
2、自变量趋于
$\hspace{2em}7、注意:函数若存在左极限和右极限,需满足\lim\limits_{x\to x_0^-}f(x)=A\Leftrightarrow f(x_0^+)=f(x_0^-)=A,函数极限才存在 $
二、函数极限的性质
1、唯一性
2、局部有界性
3、局部保号性
$\hspace{6em}\therefore \frac{3A}{2} \lt 0 且\frac{A}{2} \lt 0,f(x) \lt 0,与题设条件在x_0的去心邻域内f(x)\geq 0条件冲突,故A\geq 0 $
$\hspace{6em}\therefore \frac{A}{2} \lt 0 \frac{3A}{2} \lt 0,f(x) \lt 0,与题设条件在x_0的去心邻域内f(x)\geq 0条件冲突,故A\leq 0 $
4、函数极限与数列极限的关系
第四节、无穷小与无穷大
一、无穷小
二、无穷大
第五节、极限运算法则
一、定理1
注意:不能反推,例如
2、扩展:有限个无穷小的和依旧是无穷小
二、定理2
三、定理3
四、定理4
五、定理5
六、定理6
第六节、极限存在准则 两个重要极限
一、夹逼准则
1、数列极限存在准则
2、函数极限存在准则
二、
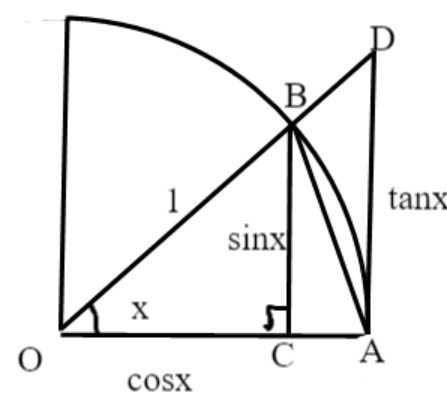
$\hspace{4em}\therefore 1 < \frac{x}{sinx} < \frac{1}{cosx} $
$\hspace{4em}\therefore cosx <\frac{sinx}{x} < 1 $
三、单调有界准则
1、单调有界数列必有极限
2、单调有界函数必有极限
四、
第二种重要极限的三种变形
五、柯西极限存在准则
第七节、无穷小的比较(比阶)
一、定义
二、定理
三、扩展
第八节、函数的连续性与间断性
一、函数的连续性
1、增量
2、定义
3、左连续和右连续
4、连续函数
5、结论
二、函数的间断性
第九节、连续函数的运算与初等函数的连续性
一、连续函数的和、差、积、商的连续性
二、 反函数与复合函数的连续性
三、初等函数的连续性
第十节、闭区间上连续函数的性质
一、有界性与最值定理
$\hspace{4em}f(x)\leq f(x_0) \Rightarrow f(x_0)是f(x)在I上的最大值 $
$\hspace{4em}f(x)\geq f(x_0) \Rightarrow f(x_0)是f(x)在I上的最小值 $
 DQ博客
DQ博客